红黑树 RBT

RBT

1. 红黑树介绍

红黑树（Red-Black Tree）是一种自平衡的二叉查找树，它保证在最坏的情况下，基本动态集合操作的时间复杂度为 $O(\log n)$ 。红黑树通过对节点着色，并在插入或删除节点时进行必要的调整，使树的高度始终保持在 $O(\log n)$ 以内，从而保证了高效的查找、插入和删除操作。

红黑树的广泛的应用

JDK 1.8 开始，HashMap 也引入了红黑树：当冲突的链表长度超过 8 时，自动转为红黑树
Java 中，TreeMap、TreeSet 都使用红黑树作为底层数据结构
Linux 底层的完全公平调度器 (CFS) 进程调度算法中，vruntime 使用红黑树进行存储。
多路复用技术的 Epoll，其核心结构是红黑树 + 双向链表。

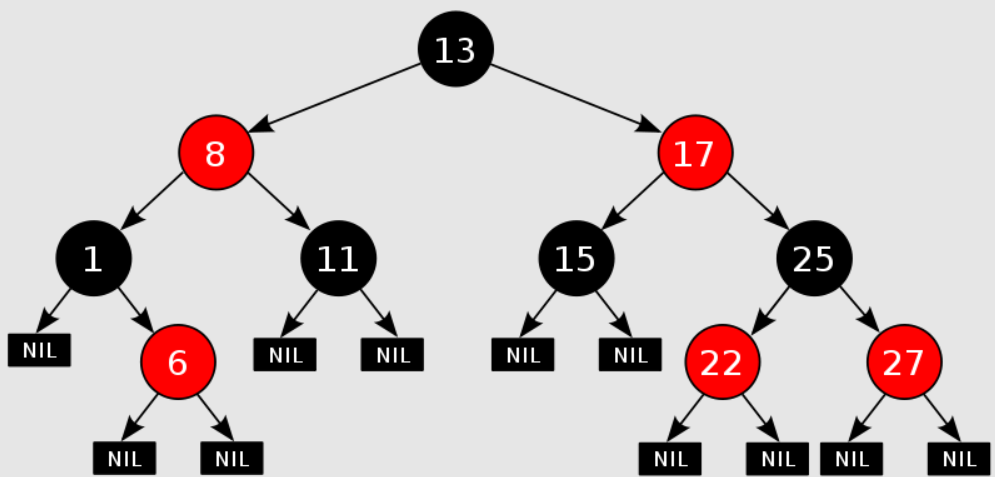
2. 红黑树的定义和性质

红黑树的每个节点都包含一个颜色属性，颜色可以是红色或黑色。红黑树的定义遵循以下五个定义：

每个节点要么是红色，要么是黑色。
根节点必须是黑色。
叶子节点都是黑色的空节点（NIL），即每个叶子节点都是一个特殊的黑色节点，没有存储实际数据。
如果一个节点是红色的，则它的两个子节点都必须是黑色的。（不能有两个连续的红色节点）
对每个节点，从该节点到 NIL 节点的所有路径上都包含相同数量的黑色节点。

这些性质确保了红黑树的高度始终保持对数增长，从而使查找、插入和删除操作的时间复杂度为 $O(\log n)$。

性质：

从根到叶子的最长的可能路径不多于最短的可能路径的两倍长
- 最短路径为全黑节点；最长为红黑相间，黑色首尾；
- 最短路径 k 个黑节点，而最长路径是 2k - 1

3. 红黑树插入

3.1 插在根节点上

直接把该节点染黑（作为根节点

3.2 插入节点的父节点是黑色

什么都不做（节点为红色

3.3 插入节点的父节点是红色

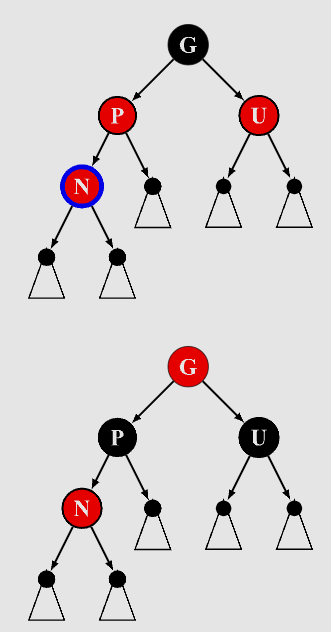
3.3.1 叔叔节点是红色

四步做完后，需要从祖父节点继续向上递归

父节点染黑
叔叔节点染黑
祖父节点染红
祖父节点设为当前节点（红色节点，即之后对当前节点进行操作，递归向上做一样的判断，直到叔叔节点不是红色

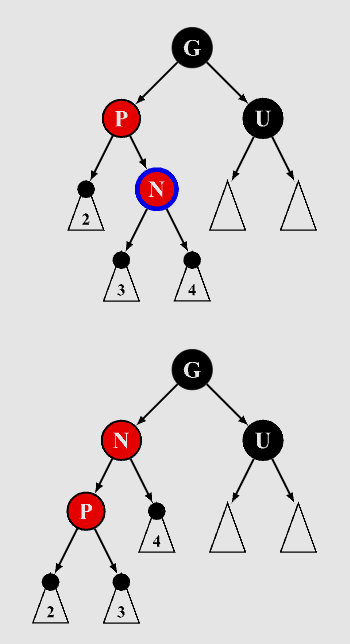
3.3.2 叔叔节点是黑色，且当前节点是其父节点的右孩子

该情况无法直接处理，需要左旋后，跳转至 3.3.3

将父节点作为新的当前节点
以新的当前节点为支点左旋

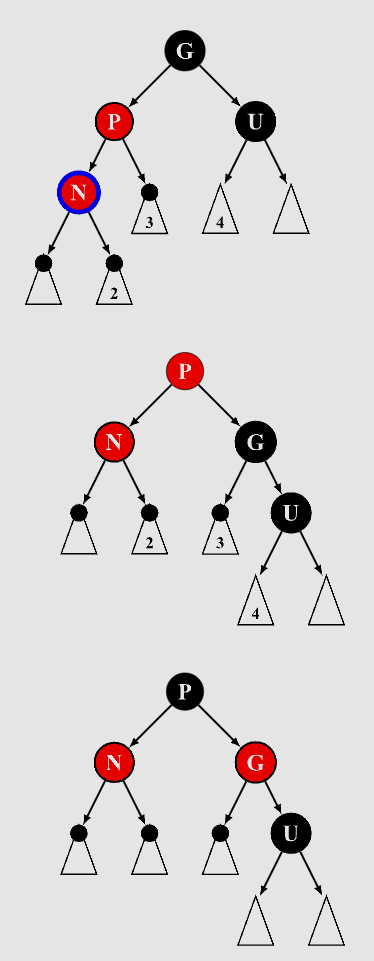
3.3.3 叔叔节点是黑色，且当前节点是其父节点的左孩子

父节点染黑
祖父节点染红
以祖父节点为支点右旋

4. 红黑树删除

4.1 删除 ”红“ + ”黑“ 节点

待删除节点有一红一黑两个子节点（NIL 为黑色也包括在内）

直接将红色的子节点染黑即可

4.2 删除根节点

根节点必然为黑色

直接将根节点染为黑即可

4.3 删除 “黑” + “黑” 节点

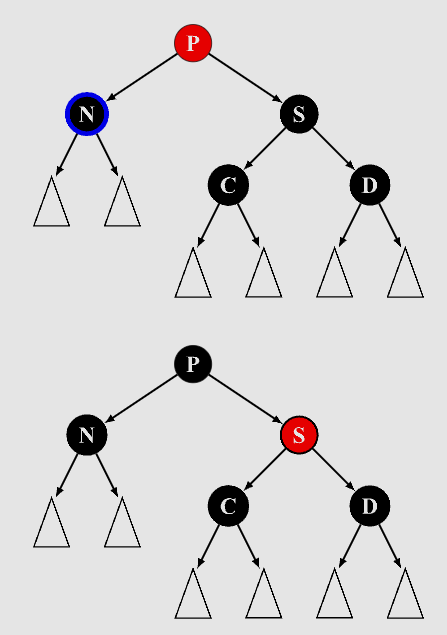
4.3.1 兄弟节点为红色

有兄弟节点，说明当前节点不是根节点，前面讨论过根节点被删除情况，后面同理。

兄弟节点染黑
父节点染红
父节点左旋
左旋后，重新设置兄弟节点为当前节点

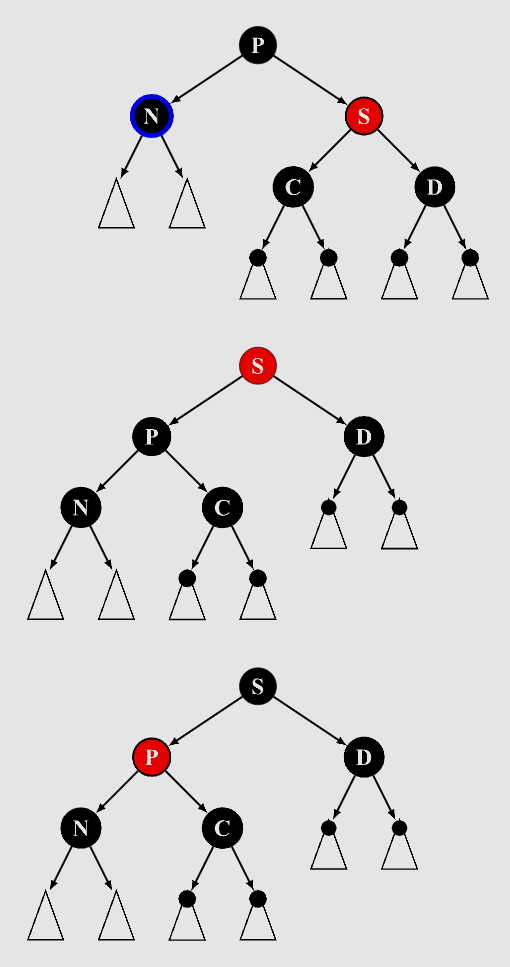
4.3.2 兄弟节点为黑色，兄弟节点的两个孩子都是黑色

兄弟节点染红
将父节点设为新的当前节点

4.3.3 兄弟节点为黑色，兄弟节点左孩子红色，右孩子黑色

兄弟节点左孩子染黑
兄弟节点染红
兄弟节点右旋
右旋后，更新旋转后的 N 的兄弟节点，即从 S 变成 C

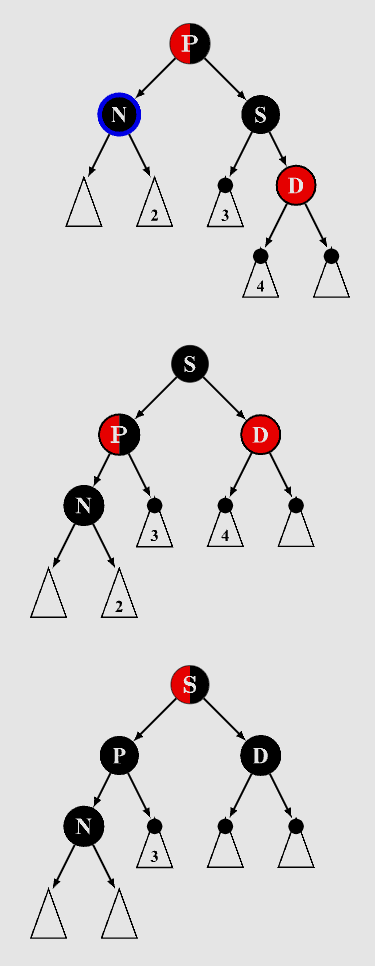
4.3.4 兄弟节点黑色，兄弟节点右孩子红色，左孩子任意颜色

父节点颜色赋值给兄弟节点
父节点染黑
兄弟节点右孩子染黑
父节点左旋
达到平衡，当前节点设为红黑树根节点即可，不再循环，已平衡

删除操作总结

4.3.1 只会执行一次，变成 2/3/4 三种情况

4.3.2 每执行一次，都会向上递归，最多执行 $log(n)$ 次，递归过程可能再遇到情况一，所以 4.3.1 也是最多 $log(n)$ 次

4.3.3 执行，会变成情况四；情况四只会执行一次

红黑树源码

一、红黑树节点定义

RBT 是个二叉树，同时还需要有颜色，颜色只有红黑两种情况，因此简单使用布尔值表示；

额外维护父节点 parent，因为插入删除需要找到兄弟或叔叔节点，需要向上遍历；

默认插入节点就是红色，原因在于：红黑树性质 5 节点到子孙节点所有路径包含相同数量黑节点，因此插入红色节点，就直接满足性质 5

1
2
3
4
5
6
7
8
9
public class Node {
    int val;
    Node left, right, parent;
    boolean red;  // 是否为红色节点, 默认为红色(false)

    public Node(int val) {
        this.val = val;
    }
}

二、红黑树定义

1
2
3
4
5
6
7
public class RedBlackTree {
    // 节点颜色
    public static final boolean RED = false;
    public static final boolean BLACK = true;

    public Node root;
}

三、红黑树搜索

就是普通二叉树的搜索

1
2
3
4
5
6
7
8
9
public Node search(int val) {
    Node x = this.root;
    while (x != null) {
        if (val == x.val) return x;
        if (val < x.val) x = x.left;
        else x = x.right;
    }
    return null;
}

四、左右旋转

该版本的左右旋转是带 parent 节点更新的，需要注意顺序

定义 x 是相对于 y 的左侧，例如左旋，则当前节点为 x，右旋则当前节点是 y

以左旋为例，整体从下到上更新，这样不会丢失指针。

先改 ly.parent = x
然后将 y 转上去，即修改 px 的孩子，如果 px 为空，该树根节点就是 y；同时修改 y.parent = px
最后更新 y 的孩子，y.left = x, x.parent = y；

3 不能在 2 之前，是因为需要通过 x.parent 找到老的 px，否则 x.parent 改为 y 后，就找不到 px 了

右旋就是左旋的镜像操作

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
// 左旋
public void leftRotate(Node x) {
    Node y = x.right;
    x.right = y.left;
    if (y.left != null)
        y.left.parent = x;
    y.parent = x.parent;

    if (x.parent == null)
        this.root = y;
    else if (x == x.parent.left)
        x.parent.left = y;
    else
        x.parent.right = y;
    y.left = x;
    x.parent = y;
}

// 右旋
public void rightRotate(Node y) {
    Node x = y.left;
    y.left = x.right;
    if (x.right != null)
        x.right.parent = y;
    x.parent = y.parent;

    if (y.parent == null)
        this.root = x;
    else if (y == y.parent.left)
        y.parent.left = x;
    else
        y.parent.right = x;
    x.right = y;
    y.parent = x;
}

五、红黑树插入

红黑树插入源码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
// 插入节点
public void insert(int val) {
    Node z = new Node(val); // 新节点, 默认红色
    z.red = RED;
    Node y = null, x = this.root;  // y 为 z 父节点(起始为空), x 为当前节点, 遍历从 x 根节点开始
    while (x != null) {
        y = x;
        if (z.val < x.val) x = x.left;
        else x = x.right;
    }
    // x 位置为 z 待插入位置, y 是其父节点
    z.parent = y;
    if (y == null) this.root = z;  // z 插入为根节点
    else if (z.val < y.val) y.left = z;
    else y.right = z;
    // 插入后的调整
    insertFixUp(z);
}

// 插入后调整
public void insertFixUp(Node z) {
    // 插入节点的父节点为红色, 需要调整(父节点为黑色什么都不做)
    while (z.parent != null && z.parent.red == RED) {
        // z 父节点是祖父节点的左孩子
        if (z.parent == z.parent.parent.left) {
            Node uncle = z.parent.parent.right;
            // 1. 叔叔节点红色
            if (uncle != null && uncle.red == RED) {
                z.parent.red = BLACK;      // 父节点染黑
                uncle.red = BLACK;         // 叔叔节点染黑
                z.parent.parent.red = RED; // 祖父节点染红
                z = z.parent.parent;       // 祖父节点作为新节点继续调整
            } else {  // 2. 叔叔节点黑色
                if (z == z.parent.right) {  // 2.1 z 是右孩子, 需要左旋到一条直线, 在 2.2 继续处理
                    z = z.parent;           // 对父节点左旋
                    leftRotate(z);
                }
                // 2.2 叔叔节点黑色, z 是左孩子
                z.parent.red = BLACK;        // 父节点染黑
                z.parent.parent.red = RED;   // 祖父节点染红
                rightRotate(z.parent.parent);// 祖父节点右旋
            }
        } else { // z 父节点是祖父节点的右孩子(右侧即左侧的镜像操作)
            Node uncle = z.parent.parent.left;
            if (uncle != null && uncle.red == RED) {
                z.parent.red = BLACK;       // 父节点染黑
                uncle.red = BLACK;          // 叔叔节点染黑
                z.parent.parent.red = RED;  // 祖父节点染红
                z = z.parent.parent;        // 祖父节点作为新节点继续调整
            } else {
                if (z == z.parent.left) {
                    z = z.parent;           // 对父节点右旋
                    rightRotate(z);
                }
                z.parent.red = BLACK;       // 父节点染黑
                z.parent.parent.red = RED;  // 祖父节点染红
                leftRotate(z.parent.parent);// 祖父节点左旋
            }
        }
    }
    this.root.red = BLACK;  // 需要保证根节点为黑色(z 插在根节点上, 需染黑)
}

六、红黑树删除

先创建一些辅助方法
- transplant，可以替换节点，主要用于 delete 节点时，将后继节点替换目标节点
- successor，可以找到节点的中序遍历较大节点值，即 successor(node)
- getColor，获取节点颜色，多封装一层 NIL 节点判定为黑色
- setColor，设置节点颜色，判空，防止空指针

辅助方法源码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
// 替换节点, v 替换 u, 只替换父索引, 不替换子索引
public void transplant(Node u, Node v) {
    if (u.parent == null) this.root = v;
    else if (u == u.parent.left) u.parent.left = v;
    else u.parent.right = v;
    if (v != null) v.parent = u.parent;
}

// 寻找子树的最小节点
public Node successor(Node node) {
    node = node.right;
    while (node.left != null) {
        node = node.left;
    }
    return node;
}

// 获取节点的颜色, 若节点为 null 则默认为黑色
private boolean getColor(Node node) {
    return node == null ? BLACK : node.red;
}

// 设置节点的颜色
public void setColor(Node node, boolean color) {
    if (node != null) node.red = color;
}

删除后的平衡调整，deleteFixup 方法，入参除了待调整节点 x，还有其父节点 parent，该 parent 存在意义在后面解释

红黑树删除操作源码

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
// 删除节点
public Node delete(int val) {
    Node node = search(val);        // 待删除节点
    if (node == null) return null;  // 待删除节点不存在
    Node y = node, x, parent;       // y 替换 node 节点, x 记录可能影响平衡的子树, parent 是 node 直接后续节点替换后 x 的父节点
    boolean originalColor = y.red;  // y 原始颜色
    if (node.left == null) {
        x = node.right;
        parent = node.parent;
        transplant(node, node.right);  // 右孩子替换 node
    } else if (node.right == null) {
        x = node.left;
        parent = node.parent;
        transplant(node, node.left);   // 左孩子替换 node
    } else {  // 找 node 直接后续节点, 替换 node 为 y(颜色与 node 同色)
        y = minimum(node);
        originalColor = y.red;
        x = y.right;             // y 会从右子树移除, 受影响平衡的是 y 的右子树
        if (y.parent == node) {  // y 是 node 的直接右孩子
            parent = y;          // 此时 x 可能是 null, 但 x 的父节点就是替换 node 的 y
        } else {                 // y 不是 node 的直接右孩子, y 右孩子替换 y
            parent = y.parent;
            transplant(y, y.right);
            y.right = node.right;
            y.right.parent = y;
        }
        transplant(node, y);  // y 替换 node
        y.left = node.left;
        y.left.parent = y;
        y.red = node.red;
    }
    node.left = node.right = node.parent = null;  // 清空 node 引用
    if (originalColor == BLACK) // y 从右子树移除到 node, 原来的 y 是黑色则需要调整(红色不影响性质)
        deleteFixup(x, parent);
    return node;
}

/**
 * 删除后, 从 x 向上修复
 *
 * @param x      修复起点, 可能为 null
 * @param parent x 的父节点
 */
public void deleteFixup(Node x, Node parent) {
    while (x != root && getColor(x) == BLACK) {
        if (x == parent.left) {        // x 是左孩子
            Node w = parent.right;     // w 是 x 的兄弟节点
            // 情况1：x 的兄弟节点 w 是红色
            if (getColor(w) == RED) {
                setColor(w, BLACK);      // 将 w 变成黑色
                setColor(parent, RED); // 将 x 的父节点变成红色
                leftRotate(parent);    // 对 x 的父节点左旋
                w = parent.right;      // 旋转后，更新兄弟节点 w
            }
            // 情况2：x 的兄弟节点 w 是黑色，且 w 的两个子节点都是黑色
            if (getColor(w.left) == BLACK && getColor(w.right) == BLACK) {
                setColor(w, RED); // 将 w 变成红色
                x = parent;     // 继续从父节点向上修复
                parent = x.parent;  // 更新 parent
            } else {
                // 情况3：w 是黑色，且 w 的右孩子是黑色，左孩子是红色
                if (getColor(w.right) == BLACK) {  // 上面判断过都为黑色, 只要右孩子是黑色, 左孩子就是红色
                    setColor(w.left, BLACK);       // 将 w 的左孩子变成黑色
                    setColor(w, RED);              // 将 w 变成红色
                    rightRotate(w);                // 对 w 右旋
                    w = parent.right;            // 旋转后，更新兄弟节点 w
                }
                // 情况4 可能由情况3 转化而来
                // 情况4：w 是黑色，且 w 的右孩子是红色
                setColor(w, getColor(parent)); // 将 w 设为父节点的颜色
                setColor(parent, BLACK);       // 将父节点设为黑色
                setColor(w.right, BLACK);        // 将 w 的右孩子设为黑色
                leftRotate(parent);            // 对 x 的父节点左旋
                x = root;                        // 修复完成，将 x 设为根节点
            }
        } else {
            // 如果 x 是右孩子，和左孩子的操作对称，交换左右操作即可
            Node w = parent.left;
            // 情况1：x 的兄弟节点 w 是红色
            if (getColor(w) == RED) {
                setColor(w, BLACK);
                setColor(parent, RED);
                rightRotate(parent);
                w = parent.left;
            }
            // 情况2：x 的兄弟节点 w 是黑色，且 w 的两个子节点都是黑色
            if (getColor(w.left) == BLACK && getColor(w.right) == BLACK) {
                setColor(w, RED);
                x = parent;
                parent = x.parent;
            } else {
                // 情况3：w 是黑色，且 w 的左孩子是黑色，右孩子是红色
                if (getColor(w.left) == BLACK) {
                    setColor(w.right, BLACK);
                    setColor(w, RED);
                    leftRotate(w);
                    w = parent.left;
                }
                // 情况4：w 是黑色，且 w 的左孩子是红色
                setColor(w, getColor(parent));
                setColor(parent, BLACK);
                setColor(w.left, BLACK);
                rightRotate(parent);
                x = root;
            }
        }
    }
    setColor(x, BLACK); // 将最终的 x 设为黑色
}

七、测试代码

验证红黑树是否符合性质

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
public boolean verifyRBTProperties() {
    return verifyProperty1(root) && verifyProperty2(root) &&
            verifyProperty4(root) && verifyProperty5(root) && verifyProperty6(root);
}

// 红黑树的性质1：每个节点是红色或黑色
private boolean verifyProperty1(Node node) {
    if (node == null) return true;  // null 节点视为黑色
    return (node.red || !node.red) && verifyProperty1(node.left) && verifyProperty1(node.right);
}

// 红黑树的性质2：根节点是黑色
private boolean verifyProperty2(Node root) {
    return root == null || root.red == BLACK;
}

// 红黑树的性质3：每个叶子节点都是黑色的空节点 null(不用验证)

// 红黑树的性质4：每个红色节点的两个子节点都是黑色
private boolean verifyProperty4(Node node) {
    if (node == null) return true;
    if (node.red == RED) {
        if (node.left != null && node.left.red == RED) return false;
        if (node.right != null && node.right.red == RED) return false;
    }
    return verifyProperty4(node.left) && verifyProperty4(node.right);
}

// 红黑树的性质5：从任一节点到其每个叶子节点的路径都包含相同数目的黑色节点
private boolean verifyProperty5(Node node) {
    return blackHeight(node) != -1;
}

// 验证是否为二叉搜索树, 中序遍历结果递增
public boolean verifyProperty6(Node root) {
    List<Integer> values = new ArrayList<>();
    inOrderTraversal(root, values);
    for (int i = 1; i < values.size(); i++) {
        if (values.get(i) < values.get(i - 1)) {
            System.out.println("Inorder traversal is not increasing: " + values);
            return false;
        }
    }
    return true;
}

// 中序遍历，将节点值添加到列表中
private void inOrderTraversal(Node node, List<Integer> values) {
    if (node == null) {
        return;
    }
    inOrderTraversal(node.left, values);
    values.add(node.val);
    inOrderTraversal(node.right, values);
}

// 计算黑高，如果黑高不一致则返回-1，代表红黑树不合法
private int blackHeight(Node node) {
    if (node == null) return 1;  // null 节点作为黑节点
    int leftBlackHeight = blackHeight(node.left);
    int rightBlackHeight = blackHeight(node.right);
    if (leftBlackHeight == -1 || rightBlackHeight == -1 || leftBlackHeight != rightBlackHeight)
        return -1;
    return leftBlackHeight + (node.red == RED ? 0 : 1);  // 红节点不计入黑高
}

打印红黑树

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
public void printTree(Node root) {
    if (root == null) return;
    LinkedList<Node> queue = new LinkedList<>();
    queue.add(root);
    while (!queue.isEmpty()) {
        int size = queue.size();
        for (int i = 0; i < size; i++) {
            Node n = queue.poll();
            String pos = n.parent == null ? "" : (n == n.parent.left ? " LE" : " RI");
            String pstr = n.parent == null ? "" : n.parent.val + "";
            String cstr = n.red == RED ? "R" : "B";
            cstr = n.parent == null ? cstr : cstr + " ";
            System.out.print(n.val + "(" + (cstr) + pstr + (pos) + ")" + "\t");
            if (n.left != null) queue.add(n.left);
            if (n.right != null) queue.add(n.right);
        }
        System.out.println();
    }
}

主函数

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
public class Solution {
    public static void main(String[] args) {
        /**
         * 红黑树插入验证
         */
        RedBlackTree tree = new RedBlackTree();
        int[] valuesToInsert = getRamdomIntArray(100);
        System.out.println("插入操作：");
        for (int value : valuesToInsert) {
            tree.insert(value);
            System.out.println("插入 " + value + " 后的树结构：");
            tree.printTree(tree.root);
            System.out.println("验证插入后的树结构是否满足红黑树性质：" + tree.verifyRBTProperties());
            System.out.println("\n-------------------------");
        }

        /**
         * 红黑树删除验证
         */
        RedBlackTree tree2 = new RedBlackTree();
        for (int value : valuesToInsert) {
            tree2.insert(value);
        }
        System.out.println("删除操作：");
        int[] valuesToDelete = getRamdomIntArray(50);
        for (int value : valuesToDelete) {
            tree2.delete(value);
            System.out.println("删除 " + value + " 后的树结构：");
            tree2.printTree(tree2.root);
            System.out.println("验证删除后的树结构是否满足红黑树性质：" + tree2.verifyRBTProperties());
            System.out.println("\n-------------------------");
        }
    }

    // 生成随机指定长度随机 int 数组
    private static int[] getRamdomIntArray(int size) {
        Random random = new Random();
        int[] arr = new int[size];
        for (int i = 0; i < size; i++) {
            arr[i] = random.nextInt(1000) + 1;
        }
        System.out.print("arr: {");
        for (int i = 0; i < size; i++) {
            System.out.print(arr[i]);
            if (i < size - 1)
                System.out.print(", ");
        }
        System.out.println("}");
        return arr;
    }
}

删除操作补充说明

双黑 null 节点无法平衡问题

下面删除操作，在左右孩子都不空的条件下，后继节点 y 会替换 node，而 y 的右孩子会替换 y；

如果 y 是 node 的直接右孩子，且 y 的右孩子是 null，在删除后的调整后，deleteFixup 的入参 x 是 null，一方面会影响到 x 找到兄弟节点（空指针异常），另一方面 x 作为 null，失去 parent 的引用，双黑节点无法向上平衡调整。

双黑 null 节点无法平衡问题源码

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
// 删除节点
public Node delete(int val) {
    Node node = search(val);        // 待删除节点
    if (node == null) return null;  // 待删除节点不存在
    Node y = node, x;  // y 替换 node 节点, x 记录可能影响平衡的子树
    boolean originalColor = y.red;  // y 原始颜色
    if (node.left == null) {
        x = node.right;
        transplant(node, node.right);  // 右孩子替换 node
    } else if (node.right == null) {
        x = node.left;
        transplant(node, node.left);   // 左孩子替换 node
    } else {
        y = successor(node);
        originalColor = y.red;
        x = y.right;
        if (y.parent == node) {  // y 是 node 的直接右孩子
            if (x != null) x.parent = y;
        }
        // y 是 node 直接右孩子, 不需要处理右侧逻辑
        if (y.parent != node) {    // y 不是 node 的直接右孩子
            // y 右孩子替换 y
            transplant(y, y.right);
            y.right = node.right;
            y.right.parent = y;
        }
        transplant(node, y);  // y 替换 node
        y.left = node.left;
        y.left.parent = y;
        y.red = node.red;
    }
    if (originalColor == BLACK) // y 是黑色, 从下面替换到上面的 node, 需要调整(红色不影响性质)
        deleteFixup(x);
    return node;
}

// 删除后调整
public void deleteFixup(Node x) {
    while (x != root && getColor(x) == BLACK) {
        if (x == x.parent.left) {        // x 是左孩子
            Node w = x.parent.right;     // w 是 x 的兄弟节点
            // 情况1：x 的兄弟节点 w 是红色
            if (getColor(w) == RED) {
                setColor(w, BLACK);      // 将 w 变成黑色
                setColor(x.parent, RED); // 将 x 的父节点变成红色
                leftRotate(x.parent);    // 对 x 的父节点左旋
                w = x.parent.right;      // 旋转后，更新兄弟节点 w
            }
            // 情况2：x 的兄弟节点 w 是黑色，且 w 的两个子节点都是黑色
            if (getColor(w.left) == BLACK && getColor(w.right) == BLACK) {
                setColor(w, RED); // 将 w 变成红色
                x = x.parent;     // 继续从父节点向上修复
            } else {
                // 情况3：w 是黑色，且 w 的右孩子是黑色，左孩子是红色
                if (getColor(w.right) == BLACK) {  // 上面判断过都为黑色, 只要右孩子是黑色, 左孩子就是红色
                    setColor(w.left, BLACK);       // 将 w 的左孩子变成黑色
                    setColor(w, RED);              // 将 w 变成红色
                    rightRotate(w);                // 对 w 右旋
                    w = x.parent.right;            // 旋转后，更新兄弟节点 w
                }
                // 情况4 可能由情况3 转化而来
                // 情况4：w 是黑色，且 w 的右孩子是红色
                setColor(w, getColor(x.parent)); // 将 w 设为父节点的颜色
                setColor(x.parent, BLACK);       // 将父节点设为黑色
                setColor(w.right, BLACK);        // 将 w 的右孩子设为黑色
                leftRotate(x.parent);            // 对 x 的父节点左旋
                x = root;                        // 修复完成，将 x 设为根节点
            }
        } else {
            // 如果 x 是右孩子，和左孩子的操作对称，交换左右操作即可
            Node w = x.parent.left;
            // 情况1：x 的兄弟节点 w 是红色
            if (getColor(w) == RED) {
                setColor(w, BLACK);
                setColor(x.parent, RED);
                rightRotate(x.parent);
                w = x.parent.left;
            }
            // 情况2：x 的兄弟节点 w 是黑色，且 w 的两个子节点都是黑色
            if (getColor(w.left) == BLACK && getColor(w.right) == BLACK) {
                setColor(w, RED);
                x = x.parent;
            } else {
                // 情况3：w 是黑色，且 w 的左孩子是黑色，右孩子是红色
                if (getColor(w.left) == BLACK) {
                    setColor(w.right, BLACK);
                    setColor(w, RED);
                    leftRotate(w);
                    w = x.parent.left;
                }
                // 情况4：w 是黑色，且 w 的左孩子是红色
                setColor(w, getColor(x.parent));
                setColor(x.parent, BLACK);
                setColor(w.left, BLACK);
                rightRotate(x.parent);
                x = root;
            }
        }
    }
    setColor(x, BLACK); // 将最终的 x 设为黑色
}

用以下 case 可以测出空指针问题

1
2
int[] valuesToInsert = {10, 20, 30, 15, 25, 5, 1};
int[] valuesToDelete = {30, 20, 10};

删除 30 后的树结构： 20(B) 10(R 20 LE) 25(B 20 RI) 5(B 10 LE) 15(B 10 RI) 1(R 5 LE)

删除 20 时，直接后继是 25，25 替换 20 后，没办法让 25 的右子树 x 替换 25，因为 x 是 null，无法指定 parent，且后续还需要针对 x 进行平衡操作，因此 x 作为双黑节点无法找到父节点和兄弟节点而无法平衡操作

解决双黑 null 节点平衡问题

相较于有问题的版本，给 deleteFixup 额外添加一个 parent 参数，用来表示 x 的父引用，这样即使在调整双黑 null 节点，也能顺利找到父节点和兄弟节点。

除此之外，deleteFixup 还需要额外添加 parent 的更新，例如情况 2，x 向 parent 移动，parent 引用也需要更新

解决双黑 null 节点平衡问题源码

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
// 删除节点
public Node delete(int val) {
    Node node = search(val);        // 待删除节点
    if (node == null) return null;  // 待删除节点不存在
    Node y = node, x, parent;       // y 替换 node 节点, x 记录可能影响平衡的子树, parent 是 node 直接后续节点替换后 x 的父节点
    boolean originalColor = y.red;  // y 原始颜色
    if (node.left == null) {
        x = node.right;
        parent = node.parent;
        transplant(node, node.right);  // 右孩子替换 node
    } else if (node.right == null) {
        x = node.left;
        parent = node.parent;
        transplant(node, node.left);   // 左孩子替换 node
    } else {  // 找 node 直接后续节点, 替换 node 为 y(颜色与 node 同色)
        y = successor(node);
        originalColor = y.red;
        x = y.right;             // y 会从右子树移除, 受影响平衡的是 y 的右子树
        if (y.parent == node) {  // y 是 node 的直接右孩子
            parent = y;          // 此时 x 可能是 null, 但 x 的父节点就是替换 node 的 y
        } else {                 // y 不是 node 的直接右孩子, y 右孩子替换 y
            parent = y.parent;
            transplant(y, y.right);
            y.right = node.right;
            y.right.parent = y;
        }
        transplant(node, y);  // y 替换 node
        y.left = node.left;
        y.left.parent = y;
        y.red = node.red;
    }
    node.left = node.right = node.parent = null;  // 清空 node 引用
    if (originalColor == BLACK) // y 从右子树移除到 node, 原来的 y 是黑色则需要调整(红色不影响性质)
        deleteFixup(x, parent);
    return node;
}

/**
 * 删除后, 从 x 向上修复
 *
 * @param x      修复起点, 可能为 null
 * @param parent x 的父节点
 */
public void deleteFixup(Node x, Node parent) {
    while (x != root && getColor(x) == BLACK) {
        if (x == parent.left) {        // x 是左孩子
            Node w = parent.right;     // w 是 x 的兄弟节点
            // 情况1：x 的兄弟节点 w 是红色
            if (getColor(w) == RED) {
                setColor(w, BLACK);      // 将 w 变成黑色
                setColor(parent, RED); // 将 x 的父节点变成红色
                leftRotate(parent);    // 对 x 的父节点左旋
                w = parent.right;      // 旋转后，更新兄弟节点 w
            }
            // 情况2：x 的兄弟节点 w 是黑色，且 w 的两个子节点都是黑色
            if (getColor(w.left) == BLACK && getColor(w.right) == BLACK) {
                setColor(w, RED); // 将 w 变成红色
                x = parent;     // 继续从父节点向上修复
                parent = x.parent;  // 更新 parent
            } else {
                // 情况3：w 是黑色，且 w 的右孩子是黑色，左孩子是红色
                if (getColor(w.right) == BLACK) {  // 上面判断过都为黑色, 只要右孩子是黑色, 左孩子就是红色
                    setColor(w.left, BLACK);       // 将 w 的左孩子变成黑色
                    setColor(w, RED);              // 将 w 变成红色
                    rightRotate(w);                // 对 w 右旋
                    w = parent.right;            // 旋转后，更新兄弟节点 w
                }
                // 情况4 可能由情况3 转化而来
                // 情况4：w 是黑色，且 w 的右孩子是红色
                setColor(w, getColor(parent)); // 将 w 设为父节点的颜色
                setColor(parent, BLACK);       // 将父节点设为黑色
                setColor(w.right, BLACK);        // 将 w 的右孩子设为黑色
                leftRotate(parent);            // 对 x 的父节点左旋
                x = root;                        // 修复完成，将 x 设为根节点
            }
        } else {
            // 如果 x 是右孩子，和左孩子的操作对称，交换左右操作即可
            Node w = parent.left;
            // 情况1：x 的兄弟节点 w 是红色
            if (getColor(w) == RED) {
                setColor(w, BLACK);
                setColor(parent, RED);
                rightRotate(parent);
                w = parent.left;
            }
            // 情况2：x 的兄弟节点 w 是黑色，且 w 的两个子节点都是黑色
            if (getColor(w.left) == BLACK && getColor(w.right) == BLACK) {
                setColor(w, RED);
                x = parent;
                parent = x.parent;
            } else {
                // 情况3：w 是黑色，且 w 的左孩子是黑色，右孩子是红色
                if (getColor(w.left) == BLACK) {
                    setColor(w.right, BLACK);
                    setColor(w, RED);
                    leftRotate(w);
                    w = parent.left;
                }
                // 情况4：w 是黑色，且 w 的左孩子是红色
                setColor(w, getColor(parent));
                setColor(parent, BLACK);
                setColor(w.left, BLACK);
                rightRotate(parent);
                x = root;
            }
        }
    }
    setColor(x, BLACK); // 将最终的 x 设为黑色
}

当然，也可以增加一个哨兵节点 NIL = new Node() ，不让叶子结点为 null，从而可以保存父引用，代码需要将所有的 null 判断全部改成 NIL 引用的判断，但是也增加了插入操作的复杂性。

JDK TreeMap 实现删除操作

参考 JDK 21 里的 java.util.TreeMap#deleteEntry 删除红黑树节点操作

TreeMap 删除操作：

待删除节点 p，如果左右孩子都存在，则找直接后继节点 s，s 值替换 p，然后 p 下移到 s
replacement 是 p 的左右非空子节点（左子树优先），p 可能是待删除节点，也可能是值替换后下移的后继节点 s。而后续的操作都是针对 replacement 删除，再调整平衡。该后续操作无论针对删除原节点 p，还是已经值替换到上面 p 的后继节点 s（s 替换 p 后 s 从 p 右子树移除），这一删除都是成立的。
replacement 不空，则代表 replacement 可以直接替换 p。注意，此时 replacement 是 p 的左右孩子其一，且非空，而 p 的另一个孩子必然为空。
1. 解释：如果 p 有两个非空孩子，则其会在一开始就会进入第一个 if，找到后继节点并值替换。然而找到的后继节点 s 左孩子必然是空的（否则会继续向左孩子遍历），只有可能有非空右孩子。而 p 一开始就没有两个非空孩子，则至多只有一个非空孩子，保证 replacement 取到一个非空孩子并进入 if (replacement != null) 块中
2. 论证 p 有且仅有一个孩子 replacement 非空（左右不重要），就可以直接将 replacement 替换 p，且只需要修改 replacement 父引用和 p.parent 子引用，不需要考虑 replacement 的另一个兄弟（null），直接简化了删除操作，变成一个单一链路的替换，而不考虑 p 可能同时被两个孩子替代
下面都是 p 无孩子情况
- 替换的 p 是根节点，直接将 root 置空（null 替换根节点）
- p 非父节点，注释中提到用 p 作为幻影替换自身，即什么都不做，先进行删除后的平衡，然后将父节点的子引用调节为 null ，实现 p 被替换的同时，也能平衡红黑树

TreeMap 删除操作源码

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
// 删除节点
public void delete(int val) {
    Node p = search(val);        // 待删除节点
    if (p == null) return;       // 待删除节点不存在

    if (p.left != null && p.right != null) {
        Node s = successor(p);
        p.val = s.val;
        p = s;
    } // p has 2 children

    // Start fixup at replacement node, if it exists.
    Node replacement = (p.left != null ? p.left : p.right);

    if (replacement != null) {
        // Link replacement to parent
        replacement.parent = p.parent;
        if (p.parent == null)
            root = replacement;
        else if (p == p.parent.left)
            p.parent.left = replacement;
        else
            p.parent.right = replacement;

        // Null out links so they are OK to use by fixAfterDeletion.
        p.left = p.right = p.parent = null;

        // Fix replacement
        if (p.red == BLACK)
            deleteFixup(replacement);
    } else if (p.parent == null) { // return if we are the only node.
        root = null;
    } else { //  No children. Use self as phantom replacement and unlink.
        if (p.red == BLACK)
            deleteFixup(p);

        if (p.parent != null) {
            if (p == p.parent.left)
                p.parent.left = null;
            else if (p == p.parent.right)
                p.parent.right = null;
            p.parent = null;
        }
    }
}

// 删除后调整
public void deleteFixup(Node x) {
    while (x != root && getColor(x) == BLACK) {
        if (x == x.parent.left) {        // x 是左孩子
            Node w = x.parent.right;     // w 是 x 的兄弟节点
            // 情况1：x 的兄弟节点 w 是红色
            if (getColor(w) == RED) {
                setColor(w, BLACK);      // 将 w 变成黑色
                setColor(x.parent, RED); // 将 x 的父节点变成红色
                leftRotate(x.parent);    // 对 x 的父节点左旋
                w = x.parent.right;      // 旋转后，更新兄弟节点 w
            }
            // 情况2：x 的兄弟节点 w 是黑色，且 w 的两个子节点都是黑色
            if (getColor(w.left) == BLACK && getColor(w.right) == BLACK) {
                setColor(w, RED); // 将 w 变成红色
                x = x.parent;     // 继续从父节点向上修复
            } else {
                // 情况3：w 是黑色，且 w 的右孩子是黑色，左孩子是红色
                if (getColor(w.right) == BLACK) {  // 上面判断过都为黑色, 只要右孩子是黑色, 左孩子就是红色
                    setColor(w.left, BLACK);       // 将 w 的左孩子变成黑色
                    setColor(w, RED);              // 将 w 变成红色
                    rightRotate(w);                // 对 w 右旋
                    w = x.parent.right;            // 旋转后，更新兄弟节点 w
                }
                // 情况4 可能由情况3 转化而来
                // 情况4：w 是黑色，且 w 的右孩子是红色
                setColor(w, getColor(x.parent)); // 将 w 设为父节点的颜色
                setColor(x.parent, BLACK);       // 将父节点设为黑色
                setColor(w.right, BLACK);        // 将 w 的右孩子设为黑色
                leftRotate(x.parent);            // 对 x 的父节点左旋
                x = root;                        // 修复完成，将 x 设为根节点
            }
        } else {
            // 如果 x 是右孩子，和左孩子的操作对称，交换左右操作即可
            Node w = x.parent.left;
            // 情况1：x 的兄弟节点 w 是红色
            if (getColor(w) == RED) {
                setColor(w, BLACK);
                setColor(x.parent, RED);
                rightRotate(x.parent);
                w = x.parent.left;
            }
            // 情况2：x 的兄弟节点 w 是黑色，且 w 的两个子节点都是黑色
            if (getColor(w.left) == BLACK && getColor(w.right) == BLACK) {
                setColor(w, RED);
                x = x.parent;
            } else {
                // 情况3：w 是黑色，且 w 的左孩子是黑色，右孩子是红色
                if (getColor(w.left) == BLACK) {
                    setColor(w.right, BLACK);
                    setColor(w, RED);
                    leftRotate(w);
                    w = x.parent.left;
                }
                // 情况4：w 是黑色，且 w 的左孩子是红色
                setColor(w, getColor(x.parent));
                setColor(x.parent, BLACK);
                setColor(w.left, BLACK);
                rightRotate(x.parent);
                x = root;
            }
        }
    }
    setColor(x, BLACK); // 将最终的 x 设为黑色
}

总结 TreeMap 删除操作精妙之处：

BST 的删除可能删除原节点 p，也可能删除后继节点 s（p 被 s 替换，s 需要从 p 的右子树删除）。方法开始就处理 p 有两孩的情况，下面的后继 s 值替换后，p 会下移至 s ，p 就变成单孩或无孩
接下来才进行真正的引用替换，只需要进行简单的两节点（p.parent, replacement ）修改引用即可，而不涉及两孩争抢 p 的问题

Reference

https://www.bilibili.com/video/BV1Ar4y1Q7Js
https://oi-wiki.org/ds/rbtree
https://tech.meituan.com/2016/12/02/redblack-tree.html
https://jingyuexing.github.io/Ebook/Algorithm/算法导论.pdf
- 《算法导论》第二版在线版，第 13 章红黑树

源码实现大部分参照《算法导论》：

非常详细的红黑树删除演示：

https://www.bilibili.com/video/BV16m421u7Tb